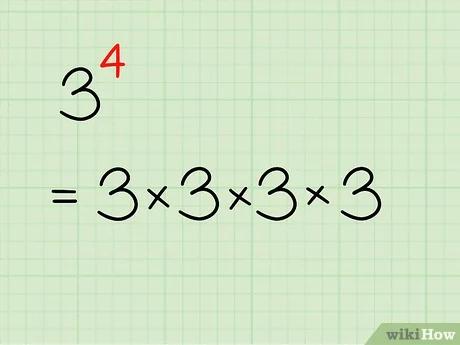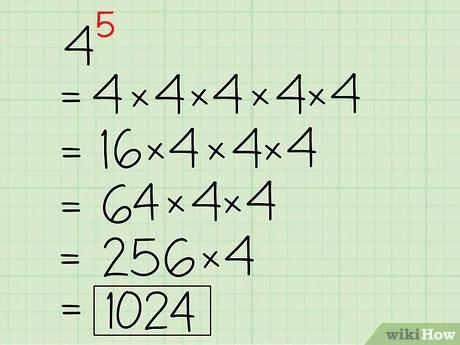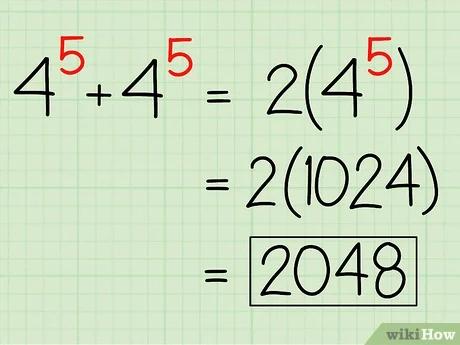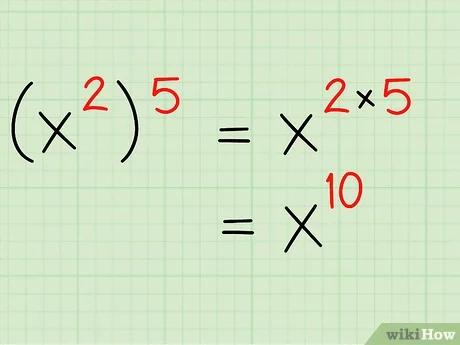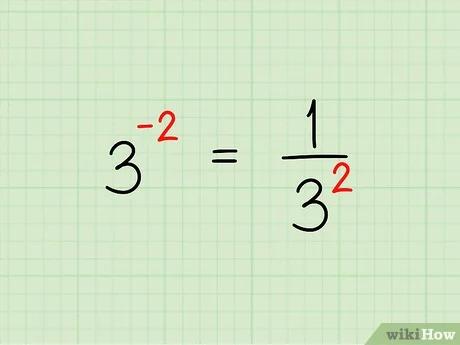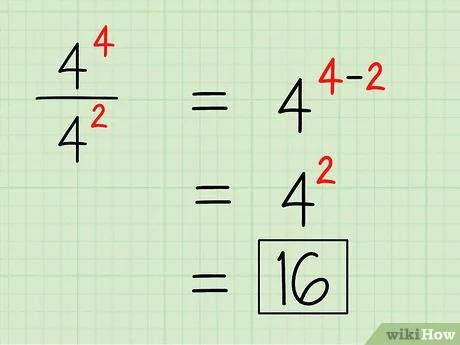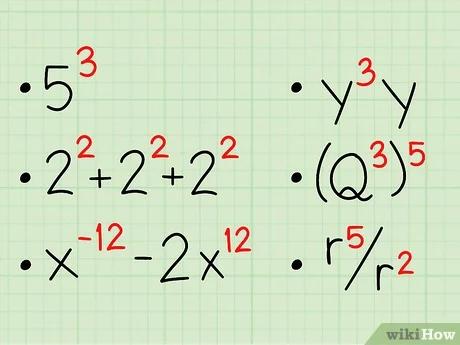كيفية حل مسائل الأسس

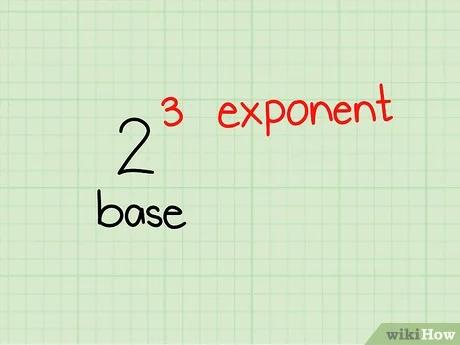
تُستَعمَل الأسس عند ضرب عدد بنفسه، فبدلًا من كتابة خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4*4*4*4*4 ، يمكنك ببساطة كتابة خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5} ، وهو ما سيشرحه هذا المقال بالتفصيل في قسمه الأول المسمى "حل أسس بسيطة". تُسهّل الأسس كتابة العبارات أو المسائل الطويلة والمعقدة، ويمكنك كذلك أن تجمع أو تطرح الأسس بسهولة لتبسيط المسائل إذا دعت الحاجة، بعد أن تتعلم قواعد جمع وطرح الأسس (مثلًا: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{2}*4^{3}=4^{5} ). ملاحظة: هذا المقال يشرح الأسس العددية؛ إذا كنت هنا لتعلم حل المعادلات الأسية التي تحتوي أسسها على قيم غير معروفة، مثل: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 2^{{2x}}=30 ، فهذا ليس المكان الصحيح؛ يمكنك البحث في جوجل عن "طريقة حل معادلات تحتوي على دوال أسية".

الخطوات

طريقة 1

طريقة 1 من 3:

حل الأسس البسيطة

Step 1 تعلم التعبيرات والمفردات الصحيحة لمسائل الأسس.

عندما تقابل عددًا أسيًا مثل خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 2^{3} ، أمامك جزأين بسيطين. العدد السفلي (الذي هو 2 هنا) يسمى الأساس، والعدد المرفوع له (وهو 3) يُعرَف باسم الأس أو القوة. فعندما نتحدث عن المثال خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 2^{3} ، نقول أن هذه "اثنان أس ثلاثة" أو "القوة الثالثة للعدد اثنين" أو "اثنان مرفوعة للقوة الثالثة".

إذا رُفِع عدد للقوة الثانية، مثل: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 5^{2} ، يمكنك أيضًا أن تقول إن هذا العدد مربع، أي "خمسة تربيع".
إذا رُفع عدد للقوة الثالثة، مثل: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 10^{3} ، يمكنك القول كذلك أنه مكعب، أي "عشرة تكعيب".
إذا لم يكن للعدد أس ظاهر، مثل رقم 4 بسيط، يعتبر في الواقع مرفوعًا للقوة الأولى ويمكن أن يُكتَب على الصورة خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{1} .
إذا كان الأس صفرًا، ورُفع "عددٌ غير صفري" لدرجة "القوة الصفرية"، فإن قيمته تساوي 1، مثل: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{0}=1 أو حتى إذا كان العدد من أي نوع آخر مثل عدد غير صحيح خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): (3/8)^{0}=1. هناك إيضاح أكثر لهذه النقطة في قسم "افكار مفيدة" في آخر المقال.

Step 2 كرر ضرب الأساس بعدد المرات الممثلة بالأس.

لحل مسألة أسس بنفسك، ابدأ بكتابتها على صورة مسألة ضرب. بما أننا ذكرنا أنك ينبغي أن تضرب الأساس في نفسه عدد مرات قيمة الأس، إذًا في حال مسألة مثل خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 3^{4} ، سوف تضرب ثلاثة كسلسلة من أربع عوامل منفصلة، أو خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 3*3*3*3 . أمثلة إضافية على هذا:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5}=4*4*4*4*4
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 8^{2}=8*8
عشرة تكعيب خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): =10*10*10

ابدأ بضرب أول عددين لتحصل على الناتج. مثال: عند حل خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5} ، سوف تضرب خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4*4*4*4*4 ، وهو ما يبدو مرهقًا إذا لم تتعامل مع المسألة خطوةً بخطوة . ابدأ بضرب أول أربعتين، ثم استبدل هاتين الأربعتين بناتج ضربهما كما سنوضح هنا:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5}=4*4*4*4*4
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4*4=16
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5}=16*4*4*4

Step 4 اضرب حاصل أول زوج أعداد (16 في هذه الحالة) في العدد التالي.

تابع ضرب الأعداد حتى "تُنمّي" الأس. متابعةً على مثالنا: سنضرب 16 في الـ 4 التالية، وهكذا:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5}=16*4*4*4
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 16*4=64
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5}=64*4*4
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 64*4=256
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5}=256*4
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 256*4=1024
نستمر كما هو موضح بضرب الأساس في حاصل ضرب أول عددين من السلسلة إلى أن تنتهي الأعداد ويكون هذا هو الناتج النهائي. باختصار: استمر بضرب أول عددين ثم اضرب الناتج في العدد التالي من التسلسل؛ ينتج عن هذه الطريقة ناتجًا صحيحًا إذا طبقتها على أي أس. الناتج الذي نصل له بعد الانتهاء من مثالنا هو خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5}=4*4*4*4*4=1024 .

Step 5 جرب حل أمثلة أخرى بيدك، وتأكد من إجابتك بعدها باستخدام آلة حاسبة.

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 8^{2}
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 3^{4}
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 10^{7}

استخدم زر "exp" أو "خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{n} " أو "^" في الآلة الحاسبة لحساب الأسس. يكاد يستحيل أن تحل مسائل أسس أكبر - مثل خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 9^{{15}} - بنفسك، لكن الآلة الحاسبة سوف توجد لك الناتج ببساطة. يظهر الزر عادةً موضح بإحدى علامات الأس المذكورة هنا. في الآلة الحاسبة في ويندوز 7، يمكن تغيير الآلة العادية في حاسوبك إلى واحدة علمية من خلال النقر على مربع "View/عرض" واختيار "Scientific/علمية"، أو الوصول في ويندوز 10 لنفس الخيار بعد النقر على الخطوط الثلاثة التي ترمز القائمة في أعلى الآلة. لإعادة الآلة عادية كما كانت، اختر "Standard" من نفس القائمة.

ابحث في جوجل عن المسألة لترَ ما إن كان الناتج الذي أوجدته صحيحًا. يمكنك استعمال رمز "^" من لوحة مفاتيح حاسوبك أو هاتفك الذكي أو الجهاز اللوحي الذي تستعمله كي تكتب العبارة الحسابية في بحث جوجل، وسوف يوجد لك هذا البحث نتيجة فورية ويظهر لك اقتراحات مسائل مشابهة لتستكشفها.

طريقة 2

طريقة 2 من 3:

جمع وطرح وضرب الأسس

Step 1 تُجمَع الأسس وتُطرَح فقط في حال تماثل الأساس والأس.

إذا كانت الأسس والأساسات متطابقة، مثل: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5}+4^{5} ، يمكنك تبسيط جمع الحدود إلى مجرد مسألة ضرب. تذكر أن خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5} يمكن اعتبارها خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 1*4^{5} وبالتالي خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5}+4^{5}=1*4^{5}+1*4^{5}=2*4^{5} من خلال جمع "1 من هذا مع 1 من ذاك = 2 من ذاك" أيًا تكن ماهية "ذاك"، وهو ما يصح عامةً في الرياضيات. اجمع فحسب عدد الحدود المتماثلة (مع الأساس والأس المتطابقين) واضرب الناتج في هذه العبارة الأسية. يمكنك ببساطة أن تحل الآن خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5} وتضرب الناتج في اثنين. تذكر أن السبب من ذلك هو أن الضرب ما هو إلا طريقة أخرى لكتابة الجمع، بما أن خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 3+3=2*3 . انظر لهذه الأمثلة:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 3^{2}+3^{2}=2*3^{2}
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5}+4^{5}+4^{5}=3*4^{5}
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{5}-4^{5}+2=2
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4x^{2}-2x^{2}=2x^{2}

Step 2 اضرب الأعداد متماثلة الأساس من خلال جمع أسسهم.

إذا كان أمامك عددين لهما نفس الأساس، مثل: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{2}*x^{5} ، كل المطلوب لجمعهما هو أن تجمع الأسين وتبقي الأساس كما هو. هكذا: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{2}*x^{5}=x^{7} . إذا كان هذا المبدأ غريبًا عليك، حلل الأعداد إلى أجزائها كي تفهم نظام هذه الفكرة بالكامل:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{2}*x^{5}
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{2}=x*x
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{5}=x*x*x*x*x
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{2}*x^{5}=(x*x)*(x*x*x*x*x)
بما أن كل ما في المسألة هو عبارة عن نفس العدد مضروبًا في نفسه لعدد من المرات، يمكننا أن نجمع ضربهم كالتالي: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{2}*x^{5}=x*x*x*x*x*x*x
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{2}*x^{5}=x^{7}

ضرب عدد أسي مرفوع لقوة أخرى مثل خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): (x^{2})^{5} . إذا كان هناك رقم مرفوع لقوة، وكلاهما مرفوعين معًا لقوة أخرى، اضرب الأسين ببساطة. إذًا: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): (x^{2})^{5}=x^{{2*5}}=x^{{10}} . كما قلنا في الخطوة السابقة؛ فكر فيما تعنيه هذه الرموز إذا شعرت أمام هذا المبدأ بصعوبة فهمه. العدد خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): (x^{2})^{5} يعني ببساطة أن نضرب خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): (x^{2}) في نفسها 5 مرات، وبالتالي:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): (x^{2})^{5}
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): (x^{2})^{5}=x^{2}*x^{2}*x^{2}*x^{2}*x^{2}
بما أن أساسات الأساس متماثلة، يمكن أن تجمعهم معًا: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): (x^{2})^{5}=x^{2}*x^{2}*x^{2}*x^{2}*x^{2}=x^{{10}}

Step 4 عامل الأسس السالبة كالكسور أو كمقلوب العدد.

إذا كنت لا تعرف ما هو المقلوب، ستتمكن من فهمه بسهولة كالتالي: إذا كان معك هذا الأس السالب خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 3^{{-2}} ، حول إشارة الكسر موجبة واجعله مقامًا لكسر بسطه الواحد، فيصبح العدد الأسي هو خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {frac {1}{3^{2}}} . إليك بعض الأمثلة الأخرى:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 5^{{-10}}{frac {1}{5^{{10}}}}
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 3x^{-}4={frac {3}{x^{4}}}

Step 5 اقسم عددين أسيين لهما نفس الأساس من خلال طرح الأسس.

القسمة عكس الضرب، ومع أن هذا لا يعني دائمًا أن طريقة حل كل منهم معاكسة للأخرى، لكنها كذلك هنا. إذا كانت المسألة التي معك هي خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {frac {4^{4}}{4^{2}}} ، اطرح ببساطة الأس العلوي ناقص السفلي واترك الأساس كما هو. بالتالي: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {frac {4^{4}}{4^{2}}}=4^{{4-2}}=4^{2} ، أو 16.

كما سترى بعد قليل، أي عدد يشكل جزءًا من كسر مثل خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {frac {1}{4^{2}}} يمكن في الحقيقة أن يُكتَب بطريقة أخرى على الصورة خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{{-2}} . الأسس السالبة تصنع كسورًا.

Step 6 جرب التدرب على بعض المسائل كي تتعود على حل الأعداد الأسية.

تغطي المسائل التالية كل ما شرحناه حتى الآن، لكي تتمكن من رؤية الإجابة، قم بالتحديد على السطر الذي توجد المسألة به بالكامل.

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 5^{3} = 125
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 2^{2}+2^{2}+2^{2} = 12
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{1}2-2x^{1}2 = -x^12
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): y^{3}*y = خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): y^{4} تذكر: العدد غير المرفوع لقوة، له أس قيمته 1
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): (Q^{3})^{5} = خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): Q^{1}5
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {frac {r^{5}}{r^{2}}} = خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): r^{3}

طريقة 3

طريقة 3 من 3:

حل أسس كسرية

تعامل مع الأسس الكسرية مثل خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{{{frac {1}{2}}}} كمسائل جذور تربيعية. العدد الأسي خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{{{frac {1}{2}}}} هو مماثل تمامًا في الواقع للعدد خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {sqrt {x}} . تستعمل هذه الطريقة دائمًا كما هي أيًا كان مقام الكسر، فالعدد خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{{{frac {1}{4}}}} هو الجذر الرابع لـ x، ويُكتب على الصورة خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {sqrt[ {4}]{x}} .

الجذور هي معكوسات الأسس. إذا أخذت مثلًا الناتج خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {sqrt[ {4}]{x}} ورفعته للقوة الرابعة، ستعود للعدد خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x ، مثلما يمكن التعامل مع خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {sqrt[ {4}]{16}}=2 على أنه خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 2^{4}=16 . على سبيل المثال أيضًا: إذا كانت خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {sqrt[ {4}]{x}}=2 فإن خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 2^{4}=x وبالتالي خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x=2 .

Step 2 حول العدد العلوي إلى أس عادي في حال كان الأس كسرًا مختلطًا.

قد تبدو المسألة خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{{{frac {5}{3}}}} مستحيلة الحل، لكنها سهلة للغاية إذا تذكرت كيف تُضرَب الأسس. حول الأساس إلى جذر كما تفعل مع الأسس الكسرية العادية، ثم ارفعه ارفع العدد بأكمله إلى القوة التي على أعلى الكسر. إذا وجدت صعوبة في تذكر هذا، فكر جيدًا في النظرية بأكملها. بمعنى أن خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {frac {5}{3}} ما هي إلا صورة أخرى لـ خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): ({frac {1}{3}})*5 مثلًا:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{{{frac {5}{3}}}}
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{{{frac {5}{3}}}}=x^{5}*x^{{{frac {1}{3}}}}
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{{{frac {1}{3}}}}={sqrt[ {3}]{x}}
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{{{frac {5}{3}}}}=x^{5}*x^{{{frac {1}{3}}}} = خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): ({sqrt[ {3}]{x}})^{5}

Step 3 اجمع واطرح واضرب الأسس الكسرية بنفس القواعد المعتادة.

من الأسهل كثيرًا أن تحاول تجمع أو تطرح الأسس قبل أن تحلها أو تحولها إلى جذور. إذا كان للعددين نفس الأساس وكانت الأسس متطابقة، يمكنك جمعهم وطرحهم كالمعتاد. كذلك يمكن ضرب وقسمة الأسس كالمعتاد عند تماثل الأساسات، طالما كنت تعرف كيفية جمع وطرح الكسور وتطبق ذلك بشكل صحيح. مثال:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{{{frac {5}{3}}}}+x^{{{frac {5}{3}}}}=2(x^{{{frac {5}{3}}}})
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): x^{{{frac {5}{3}}}}*x^{{{frac {2}{3}}}}=x^{{{frac {7}{3}}}}

أفكار مفيدة

يوجد في معظم الآلات الحاسبة زرًا تضغط عليه لكتابة الرقم كأس بعد أن تكتب الأساس كي تحل أي مسألة أسية، يكون هذا الزر على الأغلب عليه علامة مثل ^ أو س^ص (x^y).
”التبسيط" في الرياضيات يعني العمل على المسائل المعطاة لتحويل العبارات الرياضية التي بها إلى أبسط صورة ممكنة.
1 هو العنصر المحايد للأسس؛ بمعنى أن أي عدد حقيقي مرفوع للقوة الأولى (للعدد 1) هو العدد نفسه، فمثلًا: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{1}=4. ويعد الواحد كذلك عنصرًا محايدًا للضرب (يستعمل 1 كعامل مضروب به في كل الحالات، مثل في خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 5*1=5 ) وهو أيضًا العنصر المحايد في القسمة (أي عدد لا مقام له هو مقسوم على الواحد، مثل خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 5/1=5 ).
الأساس الصفري المرفوع لقوة صفرية (0) هو قيمة غير معرفة (أو يقال أحيانًا أنها لا وجود لها). إذا أدخلت مسألة كهذه إلى حاسوب أو آلة حاسبة، سيعطيك النتيجة "خطأ". تذكر كذلك أن أي عدد حقيقي غير صفري مرفوع للقوة 0 يساوي 1 دائمًا، مثل خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): 4^{0}=1.
في الجبر المتقدم للأعداد التخيلية، خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): e^{a}ix=cosax+isinax ، حيث خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تجريبي): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): i={sqrt (}-1) ، و(e) عدد ثابت غير نسبي غير منتهٍ يساوي تقريبًا 2.71828...، و(a) هي أي ثابت عشوائي (cos و sin هما بالطبع جتا وجا). يمكن إيجاد البرهان على ذلك في أي كتاب رياضيات متقدم.

تحذيرات

يتسبب زيادة الأس برفع قيمة الناتج بسرعة كبيرة، فيمكن أن تكون الإجابة صحيحة حتى لو بدت الإجابة خاطئة (يمكنك التحقق من ذلك من خلال التمثيل البياني لأي معادلة أسية، مثل: 2، إذا كان لـ x نطاق من القيم).